什么是 PyTorch?
什么是 PyTorch?
PyTorch是一个基于Python的科学计算包,提供最大灵活性和速度的深度学习研究平台。
张量
张量类似于NumPy 的n 维数组,此外张量也可以在 GPU 上使用以加速计算。
让我们构造一个简单的张量并检查输出。首先让我们看看我们如何构建一个 5×3 的未初始化矩阵:
import torch x = torch.empty(5, 3) print(x)
输出如下:
tensor([[2.7298e+32, 4.5650e-41, 2.7298e+32], [4.5650e-41, 0.0000e+00, 0.0000e+00], [0.0000e+00, 0.0000e+00, 0.0000e+00], [0.0000e+00, 0.0000e+00, 0.0000e+00], [0.0000e+00, 0.0000e+00, 0.0000e+00]])
现在让我们构造一个随机初始化的矩阵:
x = torch.rand(5, 3) print(x)
输出:
tensor([[1.1608e-01, 9.8966e-01, 1.2705e-01], [2.8599e-01, 5.4429e-01, 3.7764e-01], [5.8646e-01, 1.0449e-02, 4.2655e-01], [2.2087e-01, 6.6702e-01, 5.1910e-01], [1.8414e-01, 2.0611e-01, 9.4652e-04]])
直接从数据构造张量:
x = torch.tensor([5.5, 3]) print(x)
输出:
tensor([5.5000, 3.0000])
创建一个统一的长张量。
x = torch.LongTensor(3, 4) x tensor([[94006673833344, 210453397554, 206158430253, 193273528374], [ 214748364849, 210453397588, 249108103216, 223338299441], [ 210453397562, 197568495665, 206158430257, 240518168626]]) 「浮动张量。」 x = torch.FloatTensor(3, 4) x tensor([[-3.1152e-18, 3.0670e-41, 3.5032e-44, 0.0000e+00], [ nan, 3.0670e-41, 1.7753e+28, 1.0795e+27], [ 1.0899e+27, 2.6223e+20, 1.7465e+19, 1.8888e+31]]) 「在范围内创建张量」 torch.arange(10, dtype=torch.float) tensor([0., 1., 2., 3., 4., 5., 6., 7., 8., 9.]) 「重塑张量」 x = torch.arange(10, dtype=torch.float) x tensor([0., 1., 2., 3., 4., 5., 6., 7., 8., 9.])
使用 .view重塑张量。
x.view(2, 5) tensor([[0., 1., 2., 3., 4.], [5., 6., 7., 8., 9.]])
-1根据张量的大小自动识别维度。
x.view(5, -1) tensor([[0., 1.], [2., 3.], [4., 5.], [6., 7.], [8., 9.]]) 「改变张量轴」
改变张量轴:两种方法view和permute
view改变张量的顺序,而permute只改变轴。
x1 = torch.tensor([[1., 2., 3.], [4., 5., 6.]]) print("x1: ", x1) print(" x1.shape: ", x1.shape) print(" x1.view(3, -1): ", x1.view(3 , -1)) print(" x1.permute(1, 0): ", x1.permute(1, 0)) x1: tensor([[1., 2., 3.], [4., 5., 6.]]) x1.shape: torch.Size([2, 3]) x1.view(3, -1): tensor([[1., 2.], [3., 4.], [5., 6.]]) x1.permute(1, 0): tensor([[1., 4.], [2., 5.], [3., 6.]]) 张量运算
在下面的示例中,我们将查看加法操作:
y = torch.rand(5, 3) print(x + y)
输出:
tensor([[0.5429, 1.7372, 1.0293], [0.5418, 0.6088, 1.0718], [1.3894, 0.5148, 1.2892], [0.9626, 0.7522, 0.9633], [0.7547, 0.9931, 0.2709]])
调整大小:如果你想调整张量的形状,你可以使用“torch.view”:
x = torch.randn(4, 4) y = x.view(16) # 大小-1是从其他维度推断出来的 z = x.view(-1, 8) print(x.size(), y.size(), z.size())
输出:
torch.Size([4, 4]) torch.Size([16]) torch.Size([2, 8]) PyTorch 和 NumPy的转换
NumPy 是Python 编程语言的库,增加了对大型、多维数组和矩阵的支持,以及对这些数组进行操作的大量高级数学函数集合。
将Torch中Tensor 转换为 NumPy 数组,反之亦然是轻而易举的!
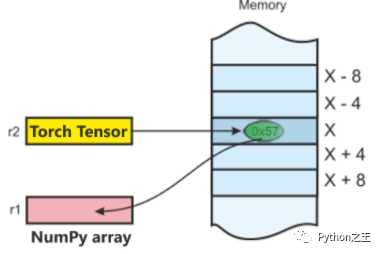
Torch Tensor 和 NumPy 数组将共享它们的底层内存位置 ,改变一个将改变另一个。
「将 Torch 张量转换为 NumPy 数组:」 a = torch.ones(5) print(a)
输出:tensor([1., 1., 1., 1., 1.])
b = a.numpy() print(b)
输出:[1., 1., 1., 1., 1.]
让我们执行求和运算并检查值的变化:
a.add_(1) print(a) print(b)
输出:
tensor([2., 2., 2., 2., 2.]) [2. 2. 2. 2. 2.] 「将 NumPy 数组转换为 Torch 张量:」 import numpy as no a = np.ones(5) b = torch.from_numpy(a) np.add(a, 1, out=a) print(a) print(b)
输出:
[2. 2. 2. 2. 2.] tensor([2., 2., 2., 2., 2.], dtype=torch.float64)
所以,正如你所看到的,就是这么简单!
接下来在这个 PyTorch 教程博客上,让我们看看PyTorch 的 AutoGrad 模块。
AutoGrad
该autograd包提供自动求导为上张量的所有操作。

它是一个按运行定义的框架,这意味着您的反向传播是由您的代码运行方式定义的,并且每次迭代都可以不同。
torch.autograd.function (函数的反向传播) torch.autograd.functional (计算图的反向传播) torch.autograd.gradcheck (数值梯度检查) torch.autograd.anomaly_mode (在自动求导时检测错误产生路径) torch.autograd.grad_mode (设置是否需要梯度) model.eval() 与 torch.no_grad() torch.autograd.profiler (提供 function 级别的统计信息) 「下面使用 Autograd 进行反向传播。」
如果requires_grad=True,则 Tensor 对象会跟踪它是如何创建的。
x = torch.tensor([1., 2., 3.], requires_grad = True) print('x: ', x) y = torch.tensor([10., 20., 30.], requires_grad = True) print('y: ', y) z = x + y print(' z = x + y') print('z:', z) x: tensor([1., 2., 3.], requires_grad=True) y: tensor([10., 20., 30.], requires_grad=True) z = x + y z: tensor([11., 22., 33.], grad_fn=)
因为requires_grad=True,z知道它是通过增加两个张量的产生z = x + y。
s = z.sum() print(s) tensor(66., grad_fn=)
s是由它的数字总和创建的。当我们调用.backward(),反向传播从s开始运行。然后可以计算梯度。
s.backward() print('x.grad: ', x.grad) print('y.grad: ', y.grad) x.grad: tensor([1., 1., 1.]) y.grad: tensor([1., 1., 1.])
下面例子是计算log(x)的导数为1 / x
import torch x = torch.tensor([0.5, 0.75], requires_grad=True) # 1 / x y = torch.log(x[0] * x[1]) y.backward() x.grad # tensor([2.0000, 1.3333])