当神经网络的研究方向逐渐转为超大规模预训练模型,研究人员的目标似乎变成了让网络拥有更大的参数量,更多的训练数据,更多样化的训练任务。
当然,这个措施确实很有效,随着神经网络越来越大,模型了解和掌握的数据也更多,在部分特定任务上已经超越人类。
但在数学上,现代神经网络的规模实际上有些过于臃肿了,参数量通常远远超过了预测任务的需求,这种情况也被称为过度参数化(overparameterization)。
NeurIPS上的一篇论文中最近就这一现象提出了一种全新的解释。他们认为这种比预期规模更大的神经网络是完全有必要的,只有这样才能避免某些基本问题,这篇论文中的发现也为这一问题提供一种更通用的见解。

论文地址:https://arxiv.org/abs/2105.12806
文章的第一作者Sébastien Bubeck在MSR Redmond管理机器学习基础研究组,主要在机器学习和理论计算机科学中跨越各种主题进行交叉研究。

神经网络就该这么大
神经网络的一项常见任务是识别图像中的目标对象。
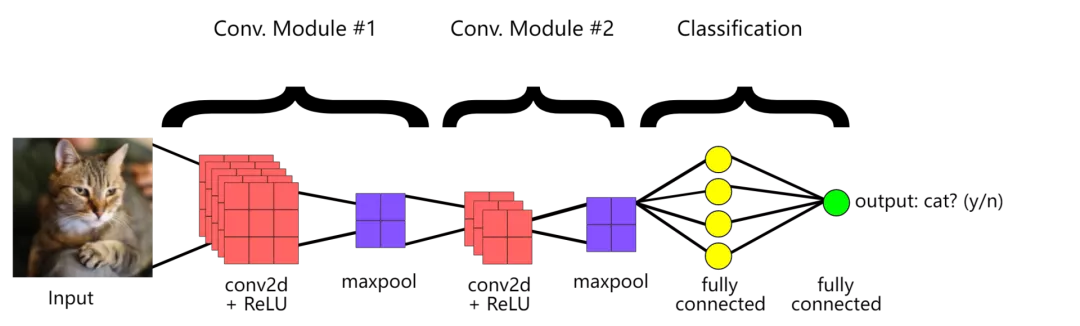
为了创建一个能够完成该任务的网络,研究人员首先为其提供许多图像和对应目标标签,对其进行训练以学习它们之间的相关性。之后,网络将正确识别它已经看到的图像中的目标。
换句话说,训练过程使得神经网络记住了这些数据。
并且,一旦网络记住了足够多的训练数据,它还能够以不同程度的准确度预测它从未见过的物体的标签,这个过程称为泛化。
网络的大小决定了它能记忆多少东西。
可以用图形化的空间来理解。假设有两个数据点,把它们放在一个XY平面上,可以用一条由两个参数描述的线来连接这些点:线的斜率和它与纵轴相交时的高度。如果其他人也知道这条直线的参数,以及其中一个原始数据点的X坐标,他们可以通过观察这条直线(或使用参数)来计算出相应的Y坐标。
也就是说,这条线已经记住了这两个数据点,神经网络做的就是差不多类似的事情。
例如,图像是由成百上千的数值描述的,每个像素都有一个对应的值。可以把这个由许多自由值组成的集合在数学上相当于高维空间中一个点的坐标,坐标的数量也称为维度。
传统的数学结论认为,要用一条曲线拟合n个数据点,你需要一个有n个参数的函数。例如,在直线的例子中,两个点是由一条有两个参数的曲线描述的。
当神经网络在20世纪80年代首次作为一种新模型出现时,研究人员也这么认为,应该只需要n个参数来适应n个数据点,而跟数据的维度无关。
德克萨斯大学奥斯汀分校的Alex Dimakis表示,现在实际情况已经不是这样了,神经网络的参数数量远远超过了训练样本的数量,这说明了教科书上的内容必须得重写进行修正。
研究人员正在研究神经网络的鲁棒性(robustness),即网络处理小变化的能力。例如,一个不鲁棒的网络可能已经学会了识别长颈鹿,但它会把一个几乎没有修改的版本误标为沙鼠。

2019年,Bubeck和同事们正在寻求证明关于这个问题的定理,当时他们就意识到这个问题与网络的规模有关。
在他们的新证明中,研究人员表明,过度参数化对于网络的鲁棒性是必要的。他们提出平滑性(smoothness),来指出需要多少个参数才能用一条具有等同于鲁棒性的数学特性的曲线来拟合数据点。
要想理解这一点,可以再次想象平面上的一条曲线,其中x坐标代表一个像素的颜色,y坐标代表一个图像标签。
由于曲线是平滑的,如果你稍微修改一下像素的颜色,沿着曲线移动一小段距离,相应的预测值只会有少量的变化。另一方面,对于一条锯齿状的曲线,X坐标(颜色)的微小变化会导致Y坐标(图像标签)的巨大变化,长颈鹿可以变成沙鼠。
Bubeck和Sellke在论文中证明,平滑拟合高维数据点不仅需要n个参数,而且需要n×d个参数,其中d是输入的维度(例如,784个像素的图像输入维度为784)。
换句话说,如果你想让一个网络稳健地记住它的训练数据,过度参数化不仅是有帮助的,而且是必须的。该证明依赖于一个关于高维几何的事实,即随机分布在球体表面的点几乎都是彼此相距一个直径的距离,点与点之间的巨大间隔意味着用一条光滑的曲线来拟合它们需要许多额外的参数。
耶鲁大学的Amin Karbasi称赞论文中的证明是非常简洁的,没有大量的数学公式,而且它说的是非常通用的内容。
这一证明结果也为理解为什么扩大神经网络的简单策略如此有效提供了一个新的途径。
其他研究揭示了过量参数化有帮助的其他原因。例如,它可以提高训练过程的效率,也可以提高网络的泛化能力。
虽然我们现在知道过量参数化对鲁棒性是必要的,但还不清楚鲁棒性对其他事情有多大必要。但通过将其与过度参数化联系起来,新的证明暗示鲁棒性可能比人们想象的更重要,这也可能为其他解释大模型的益处研究做铺垫。
鲁棒性确实是泛化的一个先决条件,如果你建立了一个系统,只是轻微地扰动它,然后它就失控了,那是什么样的系统?显然是不合理的。
所以,Bubeck认为这是一个非常基础和基本的要求。